What Is Kurtosis? | Definition, Examples & Formula

Published on June 27, 2022 by Shaun Turney. Revised on June 22, 2023.

Kurtosis is a measure of the tailedness of a distribution. Tailedness is how often outliers occur. Excess kurtosis is the tailedness of a distribution relative to a normal distribution.

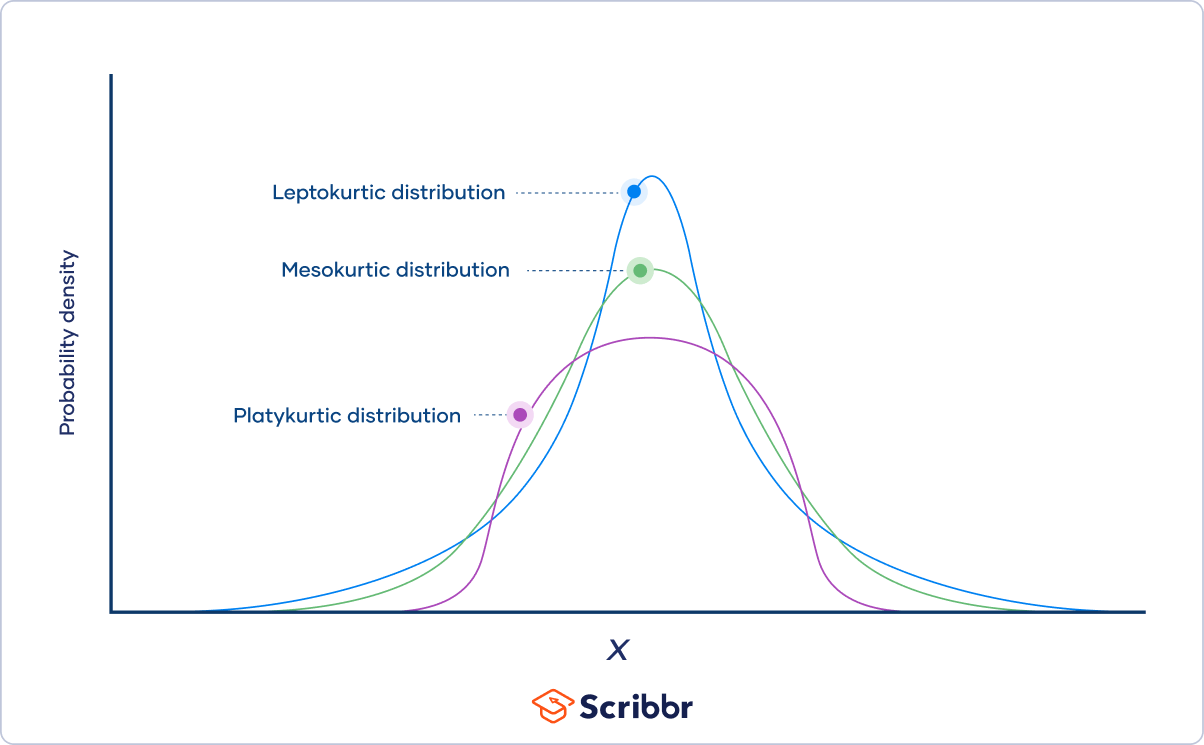
Distributions with medium kurtosis (medium tails) are mesokurtic.
Distributions with low kurtosis (thin tails) are platykurtic.
Distributions with high kurtosis (fat tails) are leptokurtic.

Tails are the tapering ends on either side of a distribution. They represent the probability or frequency of values that are extremely high or low compared to the mean. In other words, tails represent how often outliers occur.

Example: Types of kurtosis

Types of kurtosis
What is a mesokurtic distribution?
What is a platykurtic distribution?
What is a leptokurtic distribution?
How to calculate kurtosis
Other interesting articles
Frequently asked questions about kurtosis

Types of kurtosis

Distributions can be categorized into three groups based on their kurtosis:

	Category
	Mesokurtic	Platykurtic	Leptokurtic
Tailedness	Medium-tailed	Thin-tailed	Fat-tailed
Outlier frequency	Medium	Low	High
Kurtosis	Moderate (3)	Low (< 3)	High (> 3)
Excess kurtosis	0	Negative	Positive
Example distribution	Normal	Uniform	Laplace

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

What is a mesokurtic distribution?

A mesokurtic distribution is medium-tailed, so outliers are neither highly frequent, nor highly infrequent.

Kurtosis is measured in comparison to normal distributions.

Normal distributions have a kurtosis of 3, so any distribution with a kurtosis of approximately 3 is mesokurtic.

Often, kurtosis is described in terms of excess kurtosis, which is kurtosis − 3. Since normal distributions have a kurtosis of 3, excess kurtosis makes comparing a distribution’s kurtosis to a normal distribution even easier:

Normal distributions have an excess kurtosis of 0, so any distribution with an excess kurtosis of approximately 0 is mesokurtic.

Mesokurtic distribution example

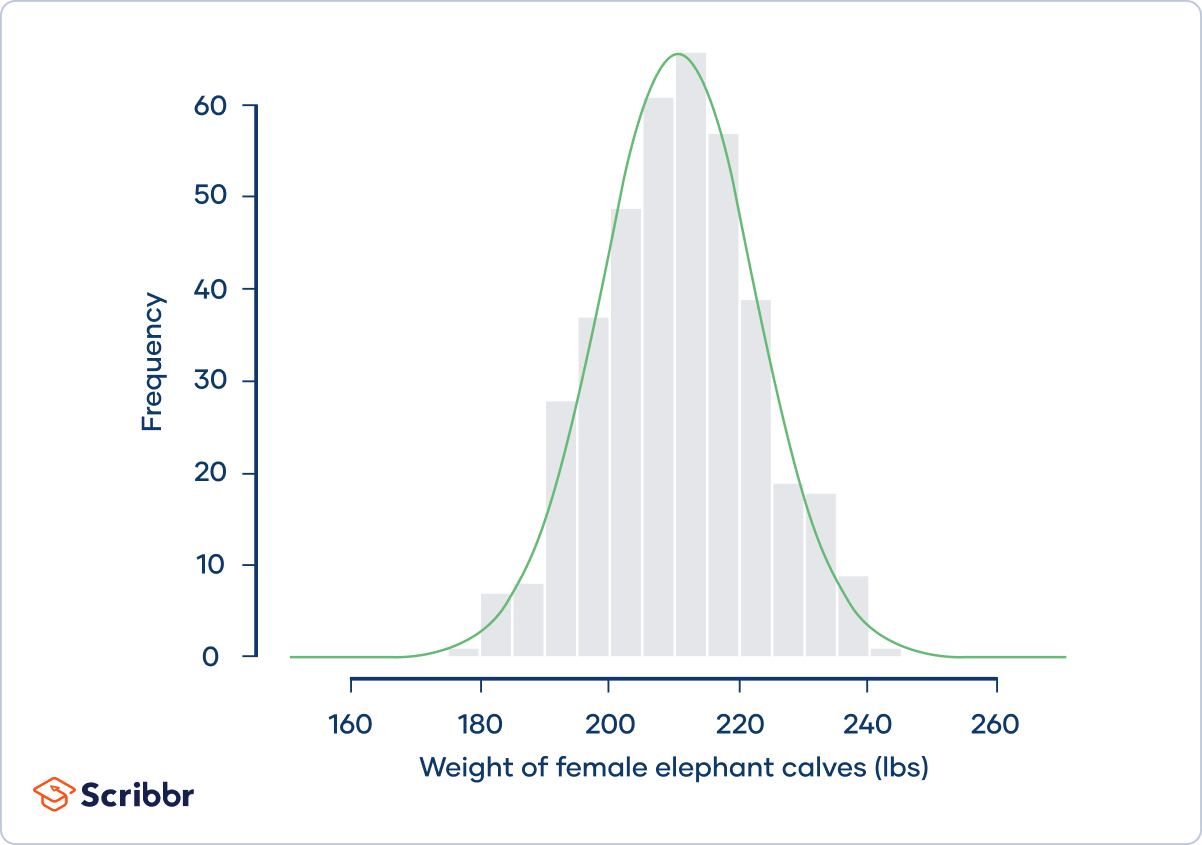
On average, a female baby elephant weighs an impressive 210 lbs at birth. Suppose that a zoologist is interested in the distribution of elephant birth weights, so she contacts zoos and sanctuaries around the world and asks them to share their data. She collects birth weight data for 400 female baby elephants:

From the graph, we can see that the frequency distribution (shown by the gray bars) approximately follows a normal distribution (shown by the green curve). Normal distributions are mesokurtic.

The zoologist calculates the kurtosis of the sample. She finds that the kurtosis is 3.09 and the excess kurtosis is 0.09, and she concludes that the distribution is mesokurtic.

Note

Although a population’s probability distribution can have a kurtosis of exactly 3, real data is almost always at least slightly platykurtic or leptokurtic. If a sample has a kurtosis of approximately 3, you can assume it’s drawn from a mesokurtic population.

Mesokurtic distributions have outliers that are neither highly frequent, nor highly infrequent, and this is true of the elephant birth weights. Occasionally, a female baby elephant will be born weighing less than 180 or more than 240 lbs.

What is a platykurtic distribution?

A platykurtic distribution is thin-tailed, meaning that outliers are infrequent.

Platykurtic distributions have less kurtosis than a normal distribution. In other words, platykurtic distributions have:

A kurtosis of less than 3
An excess kurtosis of less than 0

Platykurtosis is sometimes called negative kurtosis, since the excess kurtosis is negative.

Note

The “platy” in “platykurtosis” comes from the Greek word platús, which means flat. Although many platykurtic distributions have a flattened peak, some platykurtic distributions have a pointy peak. Statisticians now understand that kurtosis is a measure of tailedness, not “peakedness.”

A trick to remember the meaning of “platykurtic” is to think of a platypus with a thin tail.

Platykurtic distribution example

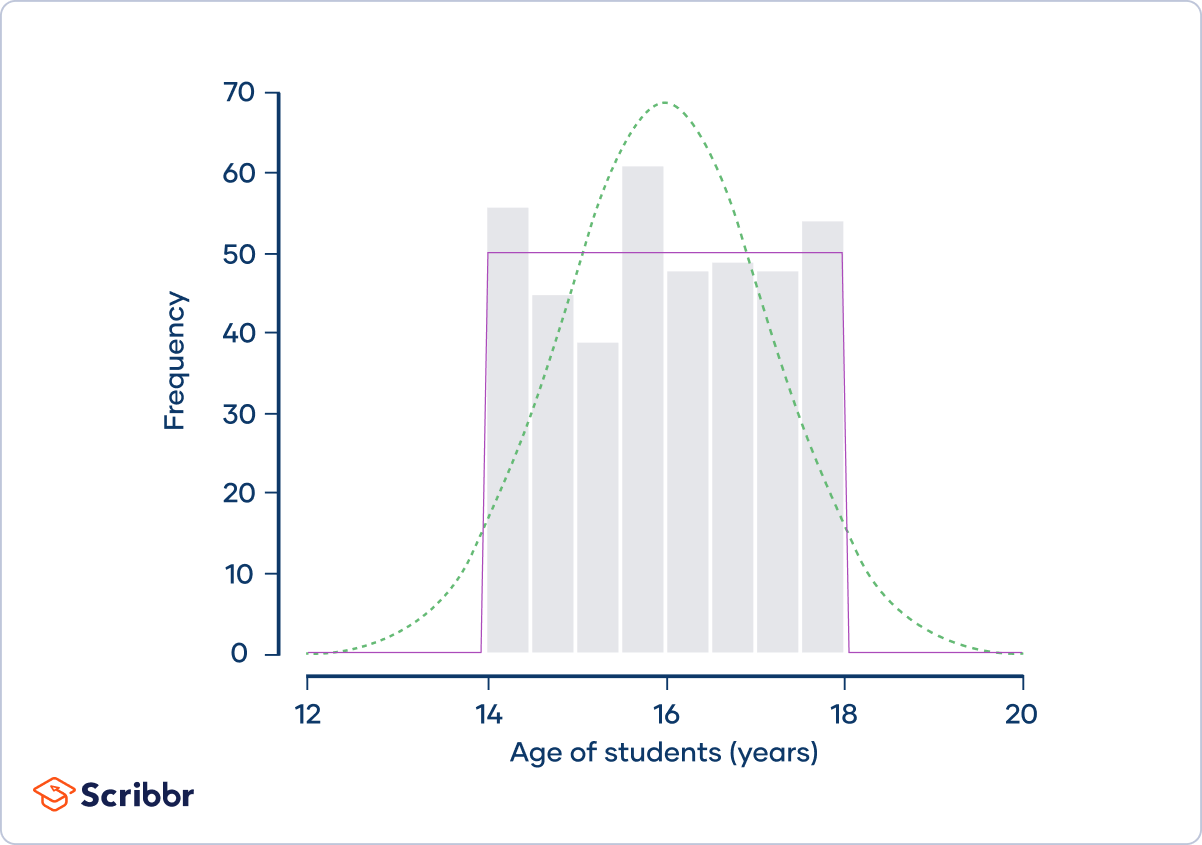
A sociologist is studying the social media use of students at a small high school. There are 400 students at the school, ranging in age from 14 to 18 years old:

The frequency distribution (shown by the gray bars) doesn’t follow a normal distribution (shown by the dotted green curve). Instead, it approximately follows a uniform distribution (shown by the purple curve). Uniform distributions are platykurtic.

The sociologist calculates that the kurtosis of the sample is 1.78 and its excess kurtosis is −1.22. He concludes that the distribution is platykurtic.

Platykurtic distributions have a low frequency of outliers. Uniform distributions, like the distribution of students’ ages, are the extreme cases of platykurtic distributions because outliers are so rare that they’re completely absent. There are no students younger than 14 or older than 18 years.

Note

In the graph above, notice that on the far left and right sides of the distribution—the tails—the space below the uniform distribution curve (purple) is thinner than the space below the normal distribution curve (green). This is what is meant by “thin tails.”

What is a leptokurtic distribution?

A leptokurtic distribution is fat-tailed, meaning that there are a lot of outliers.

Leptokurtic distributions are more kurtotic than a normal distribution. They have:

A kurtosis of more than 3
An excess kurtosis of more than 0

Leptokurtosis is sometimes called positive kurtosis, since the excess kurtosis is positive.

Note

The “lepto” in “leptokurtosis” comes from the Greek word leptós, which means narrow. Like platykurtosis, this is a misnomer because it defines kurtosis in terms of “peakedness” instead of tailedness.

A trick to remember the meaning of “leptokurtic” is to think of a leaping kangaroo with a fat tail.

Leptokurtic distribution example

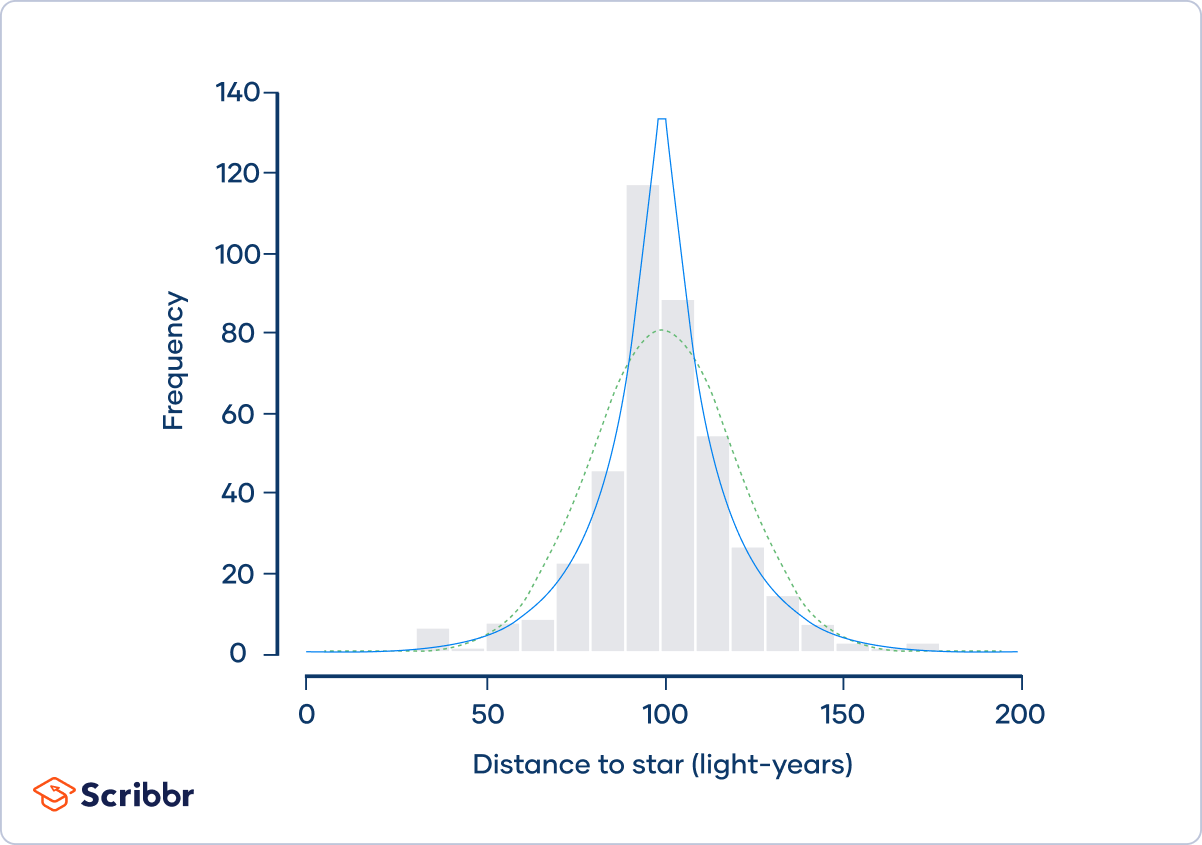
Imagine that four astronomers are all trying to measure the distance between the Earth and Nu2 Draconis A, a blue star that’s part of the Draco constellation. Each of the four astronomers measures the distance 100 times, and they put their data together in the same dataset:

The frequency distribution (shown by the gray bars) doesn’t follow a normal distribution (shown by the dotted green curve). Instead, it approximately follows a Laplace distribution (shown by the blue curve). Laplace distributions are leptokurtic.

The astronomers calculate that the kurtosis of the sample is 6.54 and its excess kurtosis is 3.54. They conclude that the distribution is leptokurtic.

Leptokurtic distributions have frequent outliers. The distribution of the astronomers’ measurements has more outliers than you would expect if the distribution were normal, with several extreme observations that are less than 50 or more than 150 light-years.

Note

If you look closely at the graph above, you’ll notice that on the far left and right sides of the distribution—the tails—the space below the Laplace distribution curve (blue) is slightly thicker than the space below the normal distribution curve (green). This is what is meant by “fat tails.”

Prevent plagiarism. Run a free check.

Try for free

How to calculate kurtosis

Mathematically speaking, kurtosis is the standardized fourth moment of a distribution. Moments are a set of measurements that tell you about the shape of a distribution.

Moments are standardized by dividing them by the standard deviation raised to the appropriate power.

Kurtosis of a population

The following formula describes the kurtosis of a population:

$\begin{equation*} \textup{kurtosis}=\tilde{\mu}_4=\dfrac{\mu_4}{\sigma^4} \end{equation*}$

Where:

$\tilde{\mu}_4$ is the standardized fourth moment
$\mu_4$ is the unstandardized central fourth moment
$\sigma$ is the standard deviation

Kurtosis of a sample

The kurtosis of a sample is an estimate of the kurtosis of the population.

It might seem natural to calculate a sample’s kurtosis as the fourth moment of the sample divided by its standard deviation to the fourth power. However, this leads to a biased estimate.

The formula for the unbiased estimate of excess kurtosis includes a lengthy correction based on the sample size:

$\begin{equation*}\textup{kurtosis}=\dfrac{(n+1)n(n-1)}{(n-1)(n-3)}\dfrac{\sum{(x_i-\bar{x})^4}}{(\sum{(x_i-\bar{x})^2})^2}-3\dfrac{(n-1)^2}{(n-2)(n-3)}\end{equation*}$

Where

$n$ is the sample size
$x_i$ are observations of the variable $x$
$\bar{x}$ is the mean of the variable $x$

It’s time-consuming to calculate kurtosis by hand. For this reason, most people use computer software to calculate it. For example, the KURT() function in Excel calculates kurtosis using the above formula.

Frequently asked questions about kurtosis

What is the difference between skewness and kurtosis?: Skewness and kurtosis are both important measures of a distribution’s shape.

Skewness measures the asymmetry of a distribution.

Kurtosis measures the heaviness of a distribution’s tails relative to a normal distribution.
What are the three categories of kurtosis?: The three categories of kurtosis are:

Mesokurtosis: An excess kurtosis of 0. Normal distributions are mesokurtic.

Platykurtosis: A negative excess kurtosis. Platykurtic distributions are thin-tailed, meaning that they have few outliers.

Leptokurtosis: A positive excess kurtosis. Leptokurtic distributions are fat-tailed, meaning that they have many outliers.
What is a normal distribution?: In a normal distribution, data are symmetrically distributed with no skew. Most values cluster around a central region, with values tapering off as they go further away from the center.

The measures of central tendency (mean, mode, and median) are exactly the same in a normal distribution.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Turney, S. (2023, June 22). What Is Kurtosis? | Definition, Examples & Formula. Scribbr. Retrieved November 3, 2023, from https://www.scribbr.com/statistics/kurtosis/

Cite this article

Is this article helpful?

You have already voted. Thanks :-) Your vote is saved :-) Processing your vote...

Shaun Turney

During his MSc and PhD, Shaun learned how to apply scientific and statistical methods to his research in ecology. Now he loves to teach students how to collect and analyze data for their own theses and research projects.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes

Generate accurate citations for free

Proofreading & Editing

AI Proofreader

Plagiarism Checker

Citation Generator

Paraphraser

Grammar Checker

What Is Kurtosis? | Definition, Examples & Formula

Table of contents

Types of kurtosis

Here's why students love Scribbr's proofreading services